- 数検3級ってどんな内容?
- どんな問題集を使えば合格できる?
- 3級の勉強法はどうすればいい?
 あや
あやそんな疑問に、この記事でバッチリ答えます!
数検3級は、中学数学の総まとめ。
中学3年間で学ぶ内容すべてが出題範囲となり、中1・中2で学んだ内容を忘れていると、思わぬ失点につながることもあります。
東大生の息子は、中学1年生の11月に数検3級を受験しました。
最初は「範囲が広すぎて無理かも…」と不安もありましたが、計画的に勉強を進めたことで自信を持って本番に臨み、無事に合格できました。
この記事では、数検3級受験の様子や使った問題集、具体的な勉強法、得点などをわかりやすく紹介します。
- 数検3級の概要や出題範囲
- 3級の合格基準や合格率の目安
- 実際に使ったおすすめ問題集と勉強法
これから数検3級の受験を考えている方に、役立つ情報をまとめました。ぜひ最後まで読んで参考にしてください。



僕の試験結果や勉強法も見てね!


私達は高卒で年収500万円台。でも、子どもは東大生に!
このブログでは、我が子が東大に合格するまでのリアルな受験体験や勉強法、受験対策を紹介しています。
プロフィールはこちら


参照:日本数学検定協会



数検3級の合格には、お子さんの「今の学習状況」に合わせた教材選びが一番の近道です。
「まずは試験の全体像や、合格に必要なレベルを詳しく知りたい」という方は、このまま読み進めてくださいね。
もし、「とにかく今のうちの子に合う教材をパッと知りたい!」という方は、下のタイプ別診断をチェックしてみてください!
数学検定(数検)3級とは?

数学検定(日本数学検定協会が主催)は、数学・算数の実用的な力を測る資格試験です。
数検3級は、「中学校3年生程度の数学力」が求められます。
中3で学ぶ内容は、いよいよ高校入試に直結する重要単元がぎっしり。
とくに平方根・因数分解・二次方程式・相似・三平方の定理は、入試でも必ずといっていいほど出題される定番分野です。
さらに、一次方程式・連立方程式・一次関数・図形の証明など、中1・中2で学んだ知識を土台に解く問題も数多く出題されます。
数検3級に挑戦することで、合否の結果だけでなく「自分の得意・苦手」を客観的に把握できます。
また、高校受験に向けて力を伸ばすきっかけとしても活用できるのが魅力です。



ここでは、数検3級の出題範囲や合格点、合格率を詳しく解説します。
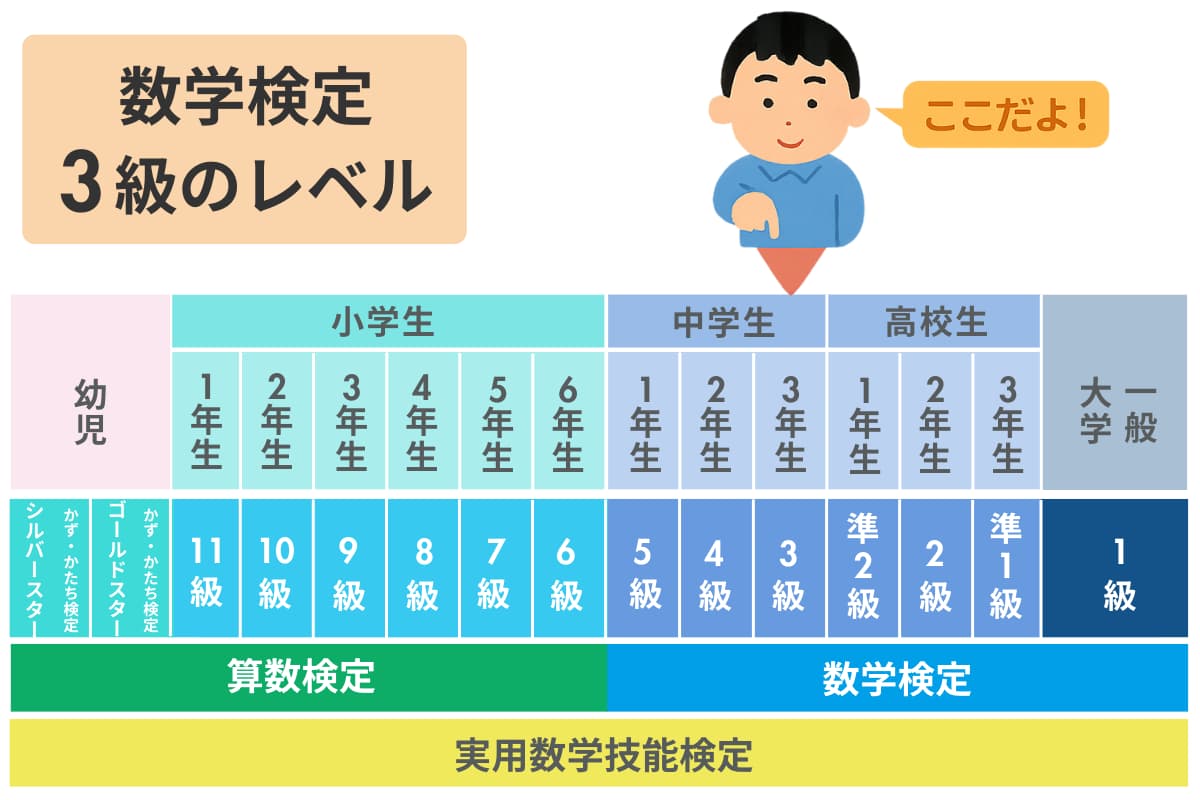
数検3級の対象学年と出題範囲
中学1年程度中学2年生程度中学3年生程度特有問題
数検3級の出題範囲と割合
3級の出題構成は、中1:30%/中2:30%/中3:30%/特有問題:10% の割合で出題されます。
| 学年 | 出題割合 | 主な内容例 |
|---|---|---|
| 中学3年程度 | 約30% | ・平方根 ・式の展開と因数分解 ・二次方程式 ・三平方の定理 ・円の性質 ・相似比 ・面積比 ・体積比 ・簡単な二次関数 ・簡単な統計 など |
| 中学2年程度 | 約30% | ・文字式を用いた簡単な式の四則混合計算 ・文字式の利用と等式の変形 ・連立方程式 ・平行線の性質 ・三角形の合同条件 ・四角形の性質 ・一次関数 ・確率の基礎 ・簡単な統計 など |
| 中学1年程度 | 約30% | ・正・負の数を含む四則混合計算 ・文字式 ・一次式の加減 ・一元一次方程式 ・基本的な作図 ・図形の移動(平行移動・対称移動・回転) ・空間図形の構成・展開 ・扇形の弧長・面積 ・柱体・錐体・球の表面積と体積 ・座標 ・比例・反比例(負の数含む) ・度数分布とヒストグラム など |
| 特有問題(応用) | 約10% | ・応用問題 |
数検3級の特有問題は「社会で創造的に活用する数学力」を問う
例えば、次のような力が求められます。
- 簡単な構造物の設計や計算ができる。
- 斜めの長さを計算することができ、材料の無駄を出すことなく切断したり行動することができる。
- 製品や社会現象を簡単な統計図で表示することができる。
数検3級の2次問題例
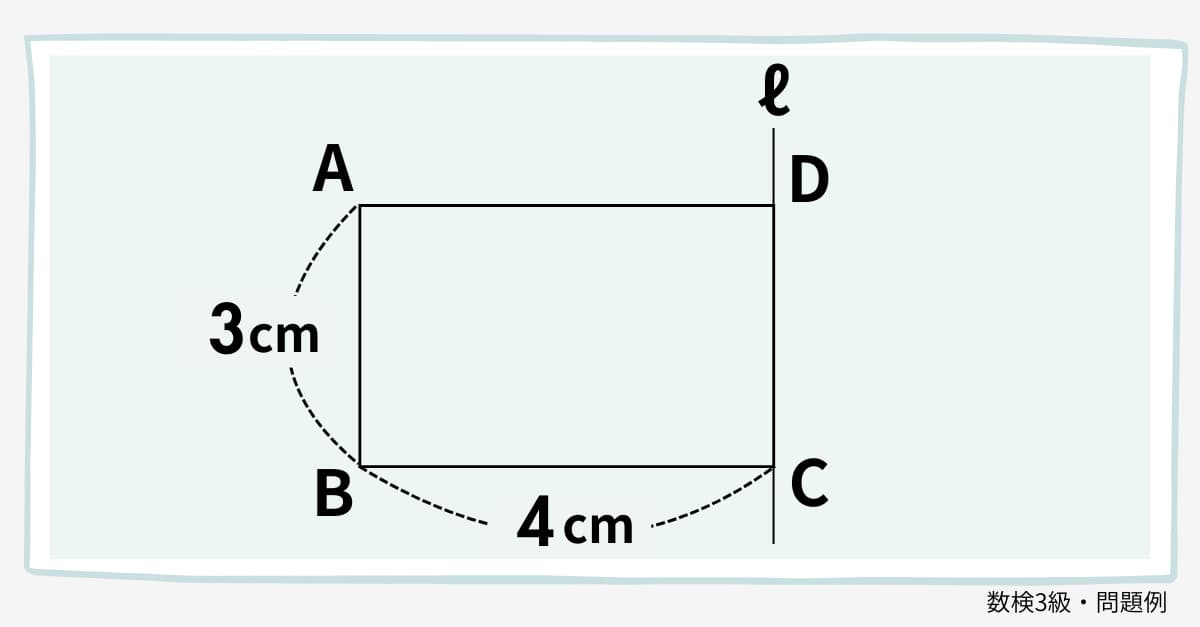

上の図のような、AB=3cm、BC=4cm の長方形を、直線 ℓ を軸として1回転させます。このときにできる円柱について、次の問いに答えなさい。ただし、円周率は πとします。
(1)底面積は何 cm² ですか。
(2)表面積は何 cm² ですか。
(3)体積は何 cm³ ですか。
答え&解説を確認する【タップする】👆
答え (1)16π cm² (2)56π cm² (3)48π cm³
解説
(1)回転させると、半径=BC=4cm、高さ=AB=3cm の円柱ができます。
求める値:半径 r = 4 cm 高さ h =3 cm として計算します。
底面は円なので、底面積=πr²=π×4² =16π cm²
(2)円柱の表面積は「側面積+底面2枚分」です。
側面積:2πrh=2π×4×3=24π
底面2枚分:2×16π=32π
合計:24π+32π=56π cm²
(3)円柱の体積は「体積=底面積 × 高さ」なので
体積:16π×3=48π cm³
数検3級では、図形や立体をイメージする力と、公式を組み合わせて活用する力が求められます。



図を書いて「どの長さが半径で、どの長さが高さか」を確認するのがコツだよ!
数学検定3級の合格点と合格率
数検3級を受験するにあたって気になるのが「どのくらい取れば合格できるの?」という点です。



ここでは、合格基準・配点、最新の合格率データ をまとめました。
数検3級の合格基準と配点
数検3級は、一次試験(計算技能検定) と 二次試験(数理技能検定) の両方で基準点をクリアする必要があります。
試験概要をまとめると、次のようになります。
| 項目 | 一次試験 (計算技能検定) | 二次試験 (数理技能検定) |
|---|---|---|
| 問題数 | 30問 | 20問 |
| 配点 | 30点満点(1問1点) | 20点満点(1問1点) |
| 合格点 | 21点以上(70%以上) | 12点以上(60%以上) |
| 検定時間 | 50分 | 60分 |



数検3級の1次と2次の違いは?



1次は、計算問題がメイン。
2次は、文章題や応用問題が出題されるんだよ。
数学検定3級の合格率は約70%!
数検3級は、例年 約65~70%の人が合格 しています。
毎年7~8万人が受験し、そのうち約5万人が合格する、最も受験者数が多い級です。
| 年度 | 合格率 |
|---|---|
| 2024年度 | 63.9% |
| 2023年度 | 67.1% |



3級はとにかく時間との勝負!
一次は1問約1分半、二次は1問約3分を目安に、ペース配分を意識しよう。
数検3級に合格!わが家の受験体験談!


ここでは、息子が実際に数学検定3級を受験したときの「得点」「当日の様子」「準備方法」を詳しくご紹介します。



わが家の体験談が、これから受験するお子さんの参考になればうれしいです。
数検3級の結果を公開!何点で合格?
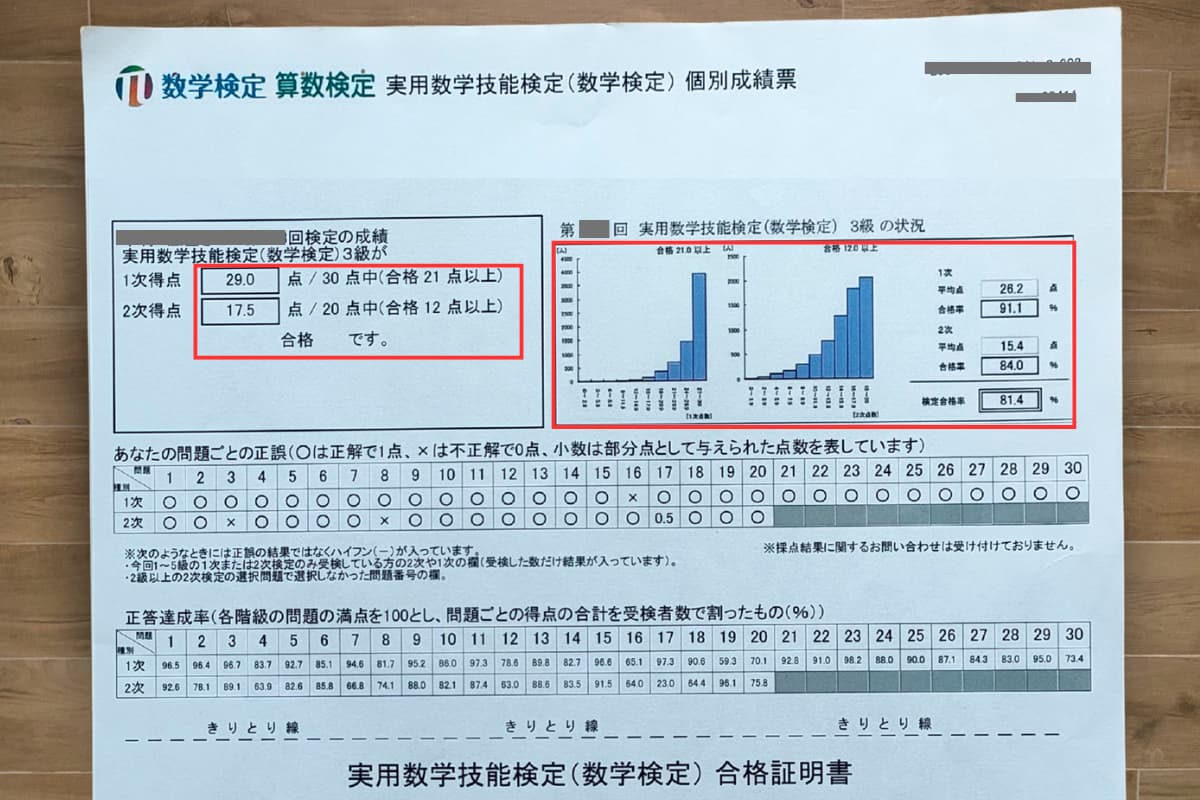

今回の得点は、 1次(29点)・2次(18点) で無事に合格できました。
| 区分 | 得点 | 平均点 | 合格ライン | 満点 |
|---|---|---|---|---|
| 1次(計算技能) | 29点 | 26.2点 | 21点 | 30点 |
| 2次(数理技能) | 17.5点 | 15.4点 | 12点 | 20点 |
一次は計算ミスで1問落としましたが、余裕をもって合格点クリア。
2次は2.5点落としやや苦戦しましたが、それでも十分合格ラインを超えることができました。
試験の必須持ち物
数検3級では「作図問題」が必ず出るので、以下の持ち物は忘れないようにしてください。
- コンパス
- 定規
- シャーペン(HB・B・2B)
- 消しゴム



8級以上は毎回コンパスを持って行ってたけど、使わなかった。
3級では、必ず出題されるから絶対に忘れないように!
数検3級を受験した時の学年
息子が3級を受験したのは、中学1年生の11月(2学期)です。
その前の4級は、小学6年生の2月に受験・合格していて、そこから約9か月後の挑戦でした。
数検3級に挑戦した理由と準備期間


数検3級(中3相当)に挑戦した理由は、小6の春に算数検定6級に合格したあと、息子が「中学生の範囲も小学生のうちに終わらせたい」と言ったことでした。
ただ、これまで先取り学習で使っていた「つみき教室のドリル(非売品)」は、6級(小6)までしか対応していないので、新しい教材を探す必要がありました。
候補に挙がったのが 進研ゼミの中1~3講座です。
漫画形式の解説や、1回15分程度で進められる分量は、小学生の息子にとっても無理なく取り組める内容でした。
しかし進研ゼミ中学講座は、5教科・9教科のセット販売で、毎月届くスタイル。今回のように「一気に先取りしたい」タイプには合いません。そこでフリマで中古教材を探し、数学だけをピックアップして使うことにしました。
結果として、中1~3年の数学の先取りはできましたが、教材を探す手間や進度の調整には正直苦労しました。



今振り返ると「もっと効率的に進められる教材もあったな」と感じています。
「じゃあ家庭でできる勉強法は?」と気になる方も多いと思います。
次のセクションでは、わが家の経験から 数検3級におすすめの勉強法 を紹介します。
数検3級のおすすめ問題集や勉強法・対策を紹介!


数検3級は「中学3年生程度の数学」が範囲です。
学校で学習した単元を終えてから受験するなら、授業や宿題をしっかり理解していれば授業の理解で十分ですが、「先取り受験」を考えているなら、基礎を固める専用の教材があると安心です。
「教材がありすぎてどれを選べばいいの?」と迷う方のために、我が家の経験をもとに、3つのタイプ別で整理しました。
| あなたのの状況は? | おすすめの 教材 | 役割・メリット |
|---|---|---|
| 確実に合格したい | 公式過去問題集 | 本番の形式に慣れる (必須!) |
| 中学数学を先取り! | スタディサプリ | 無学年制で効率よく先取り |
| 応用力をつけたい | Z会通信教育 | 難問に挑戦&記述力が伸びる |



わが家は「Z会」で土台を作り、試験前は「公式問題集」で本番に備えて合格できました! もし今、習っていない範囲がある状態からスタートするなら、スタディサプリを組み合わせるのが、一番効率が良いと感じています。
数検3級の基礎固め → Z会中学生コース
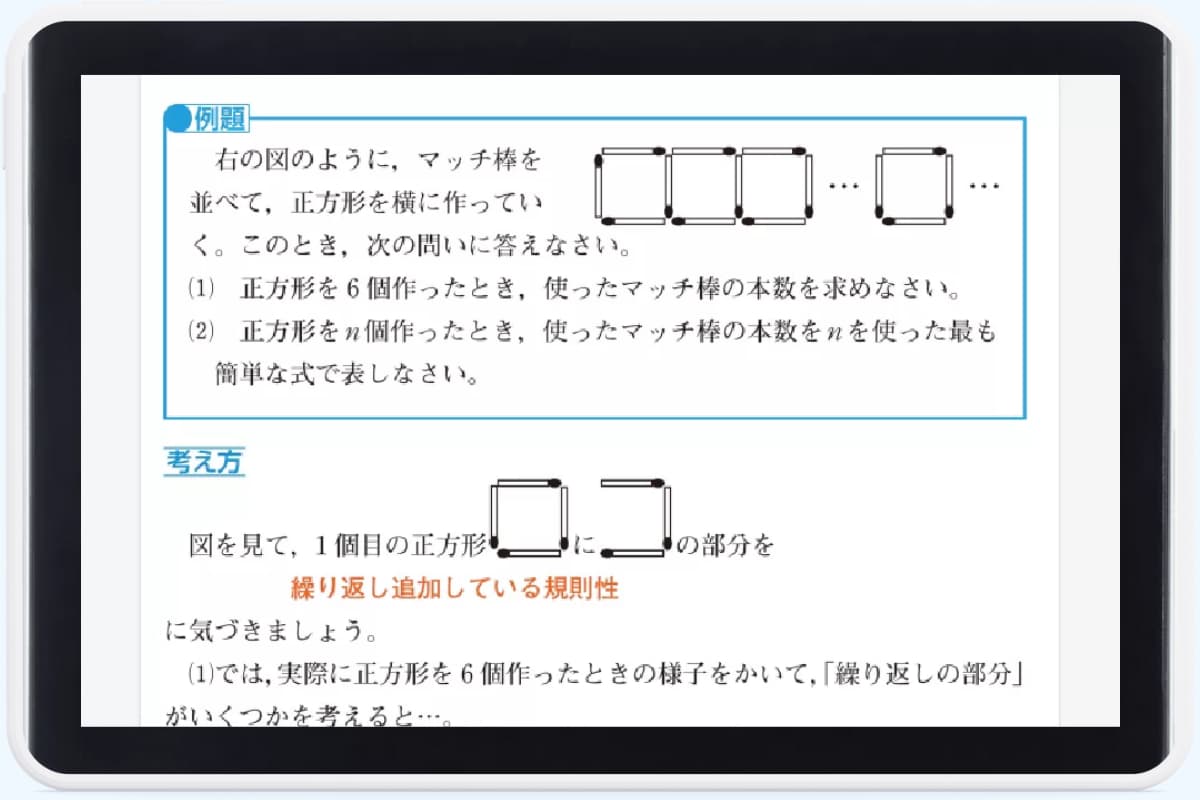

▲ 思考力・記述力を伸ばす演習問題


▲ 応用問題にも挑戦できる演習問題

▲ 解説で、重要ポイントをしっかり理解
数検3級は「中学数学の総まとめ」。
学校の進度に合わせて受験する場合でも、先取り学習で早めに挑戦する場合でも、 基礎力をしっかり固めながら応用力まで伸ばすこと が合格のカギです。
そこでおすすめなのが Z会の中学生コースです。
Z会は「ただ問題を解くだけ」で終わらず、思考力や記述力まで鍛えられる教材。数検3級の対策にとどまらず、学校の定期テストや高校受験対策にも対応できます。
Z会通信講座が役立った3つのポイント
① 基礎から応用までしっかりカバー
教科書範囲を押さえながら、応用・入試レベルの問題にも挑戦できます。
数検だけでなく、定期テストや受験に必要な力も同時に養えました。
② 記述・添削指導で理解が深まる
「なぜそうなるのか」を説明する問題が多く、論理的に考える力が自然に身につきます。
さらに添削指導で具体的なアドバイスをもらえるので、弱点克服がしやすい。
③ 1回30分程度で取り組める分量
中学生は部活や定期テストで忙しいですが、短時間で集中できる設計。
無理なく継続できたのが大きなポイントです。
息子の場合は「通信教育+過去問演習」で数検3級に挑戦しましたが、Z会で基礎を積み上げていたからこそ合格につながった と感じています。
Z会はこんな子におすすめ!
- 数検3級の合格はもちろん、高校入試も見据えた基礎・応用力を固めたい
- 応用問題や初見の問題に対して、自力で解ける「思考力」をつけたい
- 塾や部活で忙しいなかでも、自宅で効率よく質の高い演習をしたい



3級は中学数学の総仕上げ。
息子が後に数学を得意科目にできたのは、この時期にZ会でじっくり考える習慣がついたからだと思います。「数学の土台をしっかり固めておきたい」なら、Z会をぜひチェックしてみてください。
\ 今なら入会で特典がもらえる! /
資料請求は無料です
数検3級の本番対策 → 数検公式問題集
数学検定3級を確実に突破するためには、「試験の傾向を掴んで、時間内に解き切る力」が欠かせません。
3級からは2次試験の計算量も増えるため、実力があっても「時間が足りなかった…」となってはもったいないですよね。
公式問題集はこんな子におすすめ!
- 出題パターンを把握して、最短ルートで「合格」を手にしたい
- 2次試験の複雑な文章題に慣れて、確実に点数を稼ぎたい
- 本番と同じ形式で「合格ライン」に届くか、今の実力を試したい



3級は1次・2次ともに、時間配分が合否を分けます。 息子も、過去問を「本番のつもり」で繰り返し解いたことで、当日は落ち着いて取り組めたようです。 合格を確実にするなら、公式問題集でのシミュレーションが一番の近道ですよ✨
わが家が本番で9割以上を獲得できた、効率的な過去問活用ステップを紹介しますね。
過去問で全体像をつかむ
まずは「数学検定3級」の過去問題集を購入し、1回分を通して解きました。
数検は毎回似た形式なので、最初にパターンを知るだけで安心感が違います。
さらに「実用数学技能検定 文章題練習帳 数学検定3級」も追加購入。
2次試験の対策にとても役立ちました。



過去問は、最初は1回やって実力を確認!
できる・できないを仕分け
過去問を解いたら、問題を3段階で分類します。
| 記号 | 意味 | 対策方針 |
|---|---|---|
| ✅対策不要 | 過去問演習のみ | |
| ⚠️少し練習が必要 | 追加練習 | |
| ❌重点的に学習が必要 | 集中的に復習 |
❌の分野は、教科書や基礎ドリルに戻ってやり直し。



できる/できないの切り分けが、その後の勉強の効率を決めます。
弱点ごとに追加練習
仕分け後は、弱点(・❌)を集中的に反復して理解する。
過去問で力試し
追加練習のあと、再び過去問に挑戦。
理解が不十分なところはSTEP3に戻って、繰り返します。
本番形式で時間を計測
間違い直し&数日後に再挑戦
その場で間違いを直すだけでなく、数日後にもう一度やり直しました。
忘れた頃に再挑戦することで「理解したつもり」ではなく「本当に身についた」状態になります。
試験本番へ!
このサイクルを繰り返したことで、本番では9割以上を獲得できました!



合格できてすごく自信になった!



もし「まだどの教材にしようか迷っている…」という方は、冒頭で紹介した「3つのタイプ別診断」をもう一度チェックしてみてくださいね。
数検3級の先取り → スタディサプリ


数検3級をを早めに終わらせておくと、高校入試では応用問題の対策にたっぷり時間をかけられます。 さらに、そのまま高校数学の先取りへスムーズに繋げられるのも大きなメリットです。
そこで、効率よく進めたい先取り学習におすすめなのがスタディサプリ。
スタディサプリには、必要な条件がすべてそろっています。
- 小学校~高校まで無学年制で学び放題
- 1本15分の動画でテンポよく進められる
- 必要な単元だけ「戻り学習」や「先取り学習」ができる
- 月額1,815円というコスパの良さ
- 9教科すべて見放題だけど、教科を選んで学べる自由度
スタディサプリの最大の魅力は、効率よく学べる合理性にあります。
中3は部活の引退や定期テストでとにかく忙しい時期。「毎月届く教材」をこなす時間はなくても、スタサプなら必要な単元だけを動画+演習で集中して学べるので、最短距離で3級合格を目指せます。
数学はテキストだけでは理解しにくい複雑な数式も、講師の解説で「解き方のプロセス」を視覚的に理解できるため、知識が定着しやすいのが特徴です。



数学を先取りしておいたおかげで、高校受験やその先の大学受験でもすごく有利になったよ!
スタディサプリはこんな子におすすめ!
- 部活や塾で忙しく、15分のスキマ時間で効率よく3級対策をしたい
- 中1・中2の基礎に不安があり、サッと戻って復習しながら進めたい
- 「動画解説」で、難しい単元をイメージから理解したい効率派



3級の範囲は、独学だと少し手強く感じる単元も出てきます。 スタサプの神授業なら「わからない」で悩む時間を短縮できるので、忙しい中学生にこそぴったりのツールですよ✨
\ 14日間無料でお試しできます! /
※14日以内に解約すれば料金は一切かかりません。
申し込む前に、最新のキャンペーンコードを忘れずにチェックしてくださいね!
1か月無料特典など、通常より長くお試しできるチャンスがあるかもしれません✨
まとめ|数検3級の受験で感じたこと&アドバイス


数検3級の受験は、高校受験や内申点にプラスになるだけでなく、「中学数学をどれだけマスターできたか」を客観的に測れる貴重な機会です。
「せっかく受けるなら確実に合格したい!」という気持ちで準備を進める中で、大切だと感じたポイントをまとめます。
数検3級でよく出題される作図は、次の3種類です。
- 垂直二等分線
- 角の二等分線
- 点を通る垂線
作図は中1で習ったあと、中3では意外と手順を忘れがちな単元です。
実際にコンパスを使って練習しておくと、本番で焦らずに済みます。
数検3級は は問題数も増えるため、時間配分が合格のカギを握ります。
- 一次試験は、1問=約1分半
- 二次試験は、1問=約3分
- 点を通る垂線
この感覚を身につけるために、一度は必ず時計を使って「本番のつもり」で解く練習をしておきましょう。
数検3級を突破できれば、高校数学へ進むための強力な武器になります。 そして、合格という結果以上に「自分で決めて、挑戦し、やり遂げた」という経験そのものが、お子さんの大きな財産になります。
数検3級合格への第一歩は、今の生活スタイルに合った教材選びからです。
迷っている方は、もう一度この3つのタイプをチェックしてみてくださいね。



お子さんの努力が実を結び、自信に満ちた笑顔が見られるよう、心から応援しています!